Section 2 Training Data

In this section we’re going to load and explore the aerial point cloud data and RGB imagery acquired from a UAS platform which will be used for testing the slash pile detection and quantification workflow. We also have vector data including ground-truth slash pile point locations with field-measured values of pile height and diameter and image-annotated slash pile perimeters (i.e. polygons). This training data will be used in the development and statistical testing of the methodologies.

Load the standard libraries we use to do work

# bread-and-butter
library(tidyverse) # the tidyverse
library(viridis) # viridis colors
library(harrypotter) # hp colors
library(RColorBrewer) # brewer colors
library(scales) # work with number and plot scales
library(latex2exp)

# visualization
library(mapview) # interactive html maps
library(kableExtra) # tables
library(patchwork) # combine plots
library(corrplot) # correlation plots
library(ggnewscale) # new scale
library(rayshader) # Visualize Data in 2D and 3D

# spatial analysis
library(terra) # raster
library(sf) # simple features
library(lidR) # lidar data
library(rgl) # 3d plots
library(cloud2trees) # the cloud2trees
library(glcm) # textures of rasters

# modelling
library(brms)
library(tidybayes)

2.1 Slash Pile Vector Data

Slash pile field measurements were taken by measuring the height and diameter (longest side of pile) using a laser hypsometer

For volume estimation, we’ll model the ground truth slash piles as a paraboloid, specifically a parabolic dome, assuming a perfectly circular base and sides curved smoothly to a peak. Assuming a paraboloid shape is common for quantifying slash pile volume (Hardy 1996; Long & Boston 2014) and may better represent the diverse shapes of real-world slash piles than assuming a conical or half-sphere form. A paraboloid can represent a variety of shapes including those that are taller and more conical, or flatter and more spread out, because it allows the measured height and width to influence the volume calculation independently. This makes the paraboloid potentially more robust for estimating volumes of piles with varying aspect ratios.

the volume formula for a paraboloid is:

\[ V = \frac{1}{8}\pi \cdot width^2 \cdot height \]

# polygons annotated using RGB and field-collected points
slash_piles_polys <- sf::st_read(
    "../data/PFDP_Data/PFDP_SlashPiles/manitou_pile_polys.shp"
    # "f:\\PFDP_Data\\PFDP_SlashPiles\\SlashPiles_Polygons.shp"
    , quiet = T
  ) %>% 
  dplyr::rename_with(tolower) %>% 
  sf::st_make_valid() %>% 
  dplyr::filter(sf::st_is_valid(.)) %>% 
  # fix multipolygons
  dplyr::ungroup() %>% 
  dplyr::mutate(treeID = dplyr::row_number()) %>% 
  cloud2trees::simplify_multipolygon_crowns() %>% 
  dplyr::select(-c(treeID, shape_leng, shape_area))
# slash_piles_polys %>% dplyr::glimpse()

# points recorded in field
slash_piles_points <- sf::st_read(
    "../data/PFDP_Data/PFDP_SlashPiles/SlashPiles.shp"
    # "f:\\PFDP_Data\\PFDP_SlashPiles\\SlashPiles.shp"
    , quiet = T
  ) %>% 
  dplyr::rename_with(tolower) %>% 
  sf::st_zm() %>% 
  sf::st_transform(sf::st_crs(slash_piles_polys)) %>% 
  dplyr::filter( !(objectid %in% c(43)) ) %>% # duplicate field points
  dplyr::mutate(row_number = dplyr::row_number()) %>% 
  dplyr::select(-c(objectid)) %>% 
  dplyr::rename(
    height_ft = height
    , diameter_ft = diameter
  )

# stand boundary
stand_boundary <- sf::st_read("../data/PFDP_Data/Tree_Data/GIS/PFDP_Boundary.shp", quiet = T) %>% 
  sf::st_transform(sf::st_crs(slash_piles_polys)) %>% 
  sf::st_union()

what is the area of the treatment unit boundaries we are looking over?

stand_boundary %>% 
  sf::st_area() %>% 
  as.numeric() %>% 
  `/`(10000) %>% 
  scales::comma(suffix = " ha", accuracy = 0.01)

## [1] "17.48 ha"

that’s great

let’s check this on the map

# mapview::mapview(slash_piles_points, zcol = "comment", layer.name = "slash piles")
mapview::mapview(
  stand_boundary
  , color = "black"
  , lwd = 1
  , alpha.regions = 0
  , label = FALSE
  , legend = FALSE
  , popup = FALSE
  , layer.name = "stand boundary"
) +
# mapview::mapview(slash_piles_polys, zcol = "is_in_stand", layer.name = "'in' slash piles") +
mapview::mapview(slash_piles_polys, col.regions = "navy", col = NA, layer.name = "pile polys", legend = FALSE) +
mapview::mapview(slash_piles_points, cex = 2, col.regions = "gold", color = "gold", layer.name = "pile points")

because each point does not necessarily fall within the polygon boundary (e.g. due to misalignment between the imagery and point locations or slight inaccuracies in either the point or pile boundaries) we need to perform a matching process to tie the points to the polygons so that we get the height and diameter measured during the point collection attached to the polygons. to do this, we’ll use a two-stage process that first attaches the points data frame to polygons where points fall within, using a spatial intersection. It then finds and assigns the remaining, unjoined points to their nearest polygon. The final output includes all polygons from the original data, ensuring that every polygon is represented even if no points were matched.

# function to perform a two-step spatial join
  # first matching points that fall inside polygons and 
  # then assigning the remaining points to the nearest polygon
  # all original polygons are returned in the final output
match_points_to_polygons <- function(
    points_sf
    , polygons_sf
    , point_id
    , polygon_id
) {
  
  # check if point_id column exists in points_sf
  if (!point_id %in% names(points_sf)) {
    stop(paste0("column '", point_id, "' not found in points_sf."))
  }
  
  # check if polygon_id column exists in polygons_sf
  if (!polygon_id %in% names(polygons_sf)) {
    stop(paste0("column '", polygon_id, "' not found in polygons_sf."))
  }
  
  # 1. ensure the crs are the same.
  if (sf::st_crs(points_sf) != sf::st_crs(polygons_sf)) {
    points_sf <- sf::st_transform(points_sf, sf::st_crs(polygons_sf))
  }
  
  # 2. Perform a standard spatial join for points within polygons.
  # Use an inner join (`left = FALSE`) to get only points that fall inside.
  points_within <- sf::st_join(
    x = points_sf
    , y = polygons_sf
    , join = sf::st_intersects
    , left = FALSE
  )
  
  # 3. Identify points that were not matched in the first step.
  matched_points_ids <- points_within[[point_id]]
  unmatched_points <- points_sf[!points_sf[[point_id]] %in% matched_points_ids, ]
  
  if (nrow(unmatched_points) > 0) {
    # 4. For the remaining points, find the index of the nearest polygon.
    nearest_polygon_index <- sf::st_nearest_feature(unmatched_points, polygons_sf)
    
    # 5. Extract the nearest polygons and join their attributes to the unmatched points.
    nearest_polygons <- polygons_sf[nearest_polygon_index, ]
    points_nearest <- data.frame(unmatched_points, sf::st_drop_geometry(nearest_polygons))
    
    # Preserve the geometry from the original unmatched points for the nearest matches.
    points_nearest <- sf::st_set_geometry(points_nearest, sf::st_geometry(unmatched_points))
    
    # 6. Combine the results from the "points_within" and "points_nearest" joins.
    combined_points <- dplyr::bind_rows(points_within, points_nearest)
    
  } else {
    # If all points were matched in step 2.
    combined_points <- points_within
  }
  
  # 7. Perform a left join to ensure all original polygons are included in the final output.
  # Polygons without any matched points will have `NA` values for the point attributes.
  final_result <- polygons_sf %>% 
    dplyr::left_join(
      sf::st_drop_geometry(combined_points)
      , by = polygon_id
    )
  
  return(final_result)
}

we’ll also define a function to get the diameter of the polygon which we will use to extract diameter from our predicted segments to compare with the field-measured diameter values. we can also compare the field-measured diameter to the image-annotated diameter as a sanity check.

let’s define a function to get polygon diameter that accurately reflects the measurement for potentially irregular shapes. we’ll calculate the diameter by finding the maximum distance across the footprint of the entire polygon

###___________________________________________###
# calculate diameter of single polygon
###___________________________________________###
# function to calculate the diamater of an sf polygon that is potentially irregularly shaped
# using the distance between the farthest points
st_calculate_diameter_polygon <- function(polygon) {
  # get the convex hull
  ch <- sf::st_convex_hull(polygon)

  # cast to multipoint then point to get individual vertices
  ch_points <- sf::st_cast(ch, 'MULTIPOINT') %>% sf::st_cast('POINT')

  # calculate the distances between all pairs of points
  distances <- sf::st_distance(ch_points)

  # find the maximum distance, which is the diameter
  diameter <- as.numeric(max(distances,na.rm=T))
  return(diameter)
}
# apply st to sf data
st_calculate_diameter <- function(sf_data) {
  if(!inherits(sf_data,"sf")){stop("st_calculate_diameter() requires polygon sf data")}
  if(
    !all( sf::st_is(sf_data, c("POLYGON","MULTIPOLYGON")) )
  ){
    stop("st_calculate_diameter() requires polygon sf data")
  }

  # get the geometry column name
  geom_col_name <- attr(sf_data, "sf_column")

  # calculate diameter
  # !!rlang::sym() unquotes the geometry column
  return_dta <- sf_data %>% 
    dplyr::ungroup() %>% 
    dplyr::rowwise() %>%
    dplyr::mutate(diameter_m = st_calculate_diameter_polygon( !!rlang::sym(geom_col_name) )) %>%
    dplyr::ungroup()
  return(return_dta)
}

let’s apply our match_points_to_polygons() and st_calculate_diameter() functions

# nrow(slash_piles_polys)
# let's do it
slash_piles_polys <-
  match_points_to_polygons(
    points_sf = slash_piles_points 
    , polygons_sf = slash_piles_polys
    , point_id = "row_number"
    , polygon_id = "pile_id"
  ) %>% 
  dplyr::ungroup() %>%
  sf::st_make_valid() %>%
  dplyr::filter(sf::st_is_valid(.)) %>% 
  st_calculate_diameter() %>% 
  dplyr::rename(image_gt_diameter_m = diameter_m) %>% 
  # calculate area and volume
  dplyr::mutate(
    # height 
    height_m = height_ft*0.3048
    , field_diameter_m = diameter_ft*0.3048 # *0.3048 or /3.281 to convert to m
    , field_radius_m = (field_diameter_m/2)
    , image_gt_area_m2 = sf::st_area(.) %>% as.numeric()
    , field_gt_area_m2 = pi*field_radius_m^2 
    # volume ASSUMING PERFECT GEOMETRIC SHAPE :/
    , image_gt_volume_m3 = (1/8) * pi * ( (sqrt(image_gt_area_m2/pi)*2)^2 ) * height_m # (1/8) * pi * (shape_length^2) * max_height_m
      # (sqrt(image_gt_area_m2/pi)*2) = diameter assuming of circle covering same area
    , field_gt_volume_m3 = (1/8) * pi * (field_diameter_m^2) * height_m # (1/8) * pi * (shape_length^2) * max_height_m
  )
  
# check if the pile is in the stand boundary
slash_piles_polys <- slash_piles_polys %>% 
  dplyr::mutate(
    is_in_stand = pile_id %in% (slash_piles_polys %>% 
      sf::st_intersection(stand_boundary) %>% 
      sf::st_drop_geometry() %>% 
      dplyr::pull(pile_id))
  )

what?

slash_piles_polys %>% dplyr::glimpse()

## Rows: 187
## Columns: 19
## $ pile_id             <dbl> 3, 4, 5, 6, 8, 11, 13, 15, 16, 17, 19, 20, 21, 22,…
## $ comment             <chr> NA, NA, NA, NA, "Mechanical Pile", NA, NA, NA, NA,…
## $ comment2            <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
## $ height_ft           <dbl> NA, NA, NA, NA, 14.0, NA, NA, NA, NA, NA, NA, NA, …
## $ diameter_ft         <dbl> NA, NA, NA, NA, 22.0, NA, NA, NA, NA, NA, NA, NA, …
## $ xcoord              <dbl> NA, NA, NA, NA, 1019078, NA, NA, NA, NA, NA, NA, N…
## $ ycoord              <dbl> NA, NA, NA, NA, 4334862, NA, NA, NA, NA, NA, NA, N…
## $ refcorner           <chr> NA, NA, NA, NA, "G4", NA, NA, NA, NA, NA, NA, NA, …
## $ row_number          <int> NA, NA, NA, NA, 93, NA, NA, NA, NA, NA, NA, NA, NA…
## $ geometry            <POLYGON [m]> POLYGON ((499341.7 4317759,..., POLYGON ((…
## $ image_gt_diameter_m <dbl> 6.469934, 6.867876, 6.387723, 6.589466, 7.595808, …
## $ height_m            <dbl> NA, NA, NA, NA, 4.2672, NA, NA, NA, NA, NA, NA, NA…
## $ field_diameter_m    <dbl> NA, NA, NA, NA, 6.7056, NA, NA, NA, NA, NA, NA, NA…
## $ field_radius_m      <dbl> NA, NA, NA, NA, 3.3528, NA, NA, NA, NA, NA, NA, NA…
## $ image_gt_area_m2    <dbl> 25.166539, 32.028082, 22.928349, 26.261937, 28.909…
## $ field_gt_area_m2    <dbl> NA, NA, NA, NA, 35.315484, NA, NA, NA, NA, NA, NA,…
## $ image_gt_volume_m3  <dbl> NA, NA, NA, NA, 61.682109, NA, NA, NA, NA, NA, NA,…
## $ field_gt_volume_m3  <dbl> NA, NA, NA, NA, 75.34912, NA, NA, NA, NA, NA, NA, …
## $ is_in_stand         <lgl> FALSE, FALSE, FALSE, FALSE, TRUE, FALSE, FALSE, FA…

summary statistics for the form measurements

kbl_form_sum_stats <- function(
  pile_df
  , caption = "Ground Truth Piles: summary statistics for form measurements"
) {
pile_df %>% 
  sf::st_drop_geometry() %>% 
  dplyr::select(
    tidyselect::contains("height_m")
    | tidyselect::contains("diameter_m")
    | tidyselect::contains("area_m2")
    | tidyselect::contains("volume_m3")
  ) %>% 
  dplyr::summarise(
    dplyr::across(
      dplyr::everything()
      , .fns = list(
        mean = ~mean(.x,na.rm=T)
        , sd = ~sd(.x,na.rm=T)
        , q10 = ~quantile(.x,na.rm=T,probs=0.1)
        , q50 = ~quantile(.x,na.rm=T,probs=0.5)
        , q90 = ~quantile(.x,na.rm=T,probs=0.9)
        , min = ~min(.x,na.rm=T)
        , max = ~max(.x,na.rm=T)
      )
    )
    , n = dplyr::n()
  ) %>% 
  dplyr::ungroup() %>% 
  tidyr::pivot_longer(cols = -c(n)) %>% 
  dplyr::mutate(
    agg = stringr::word(name,-1,sep = "_")
    , metric = stringr::str_remove_all(name, paste0("_",agg)) %>% 
      stringr::str_extract("(paraboloid_volume|volume|area|height|diameter)") %>% 
      dplyr::coalesce("detection") %>% 
      stringr::str_c(
        dplyr::case_when(
          stringr::str_detect(name,"(field|image)") ~ paste0(" (", stringr::str_extract(name,"(field|image)"), ")")
          , T ~ ""
        )
      ) %>% 
      stringr::str_replace("area", "area m<sup>2</sup>") %>% 
      stringr::str_replace("volume", "volume m<sup>3</sup>") %>% 
      stringr::str_replace("diameter", "diameter m") %>% 
      stringr::str_replace("height", "height m") %>% 
      stringr::str_to_sentence()
  ) %>% 
  # dplyr::count(metric)
  dplyr::select(-name) %>% 
  dplyr::mutate(
    value = dplyr::case_when(
      # metric == "gt_height_m" ~ scales::comma(value,accuracy=0.1)
      T ~ scales::comma(value,accuracy=0.1)
    )
  ) %>% 
  tidyr::pivot_wider(names_from = agg, values_from = value) %>% 
  dplyr::mutate(
    range = paste0(min, "—", max)
  ) %>% 
  dplyr::arrange(desc(n)) %>% 
  dplyr::select(-c(min,max)) %>% 
  kableExtra::kbl(
    caption = caption
    , col.names = c(
      "# piles", "Metric"
      , "Mean"
      , "Std Dev"
      , "q 10%", "Median", "q 90%"
      , "Range"
    )
    , escape = F
    # , digits = 2
  ) %>% 
  kableExtra::kable_styling(font_size = 13) %>% 
  kableExtra::collapse_rows(columns = 1, valign = "top")
}

kbl_form_sum_stats(
  slash_piles_polys %>% dplyr::filter(is_in_stand) %>% dplyr::select(!tidyselect::contains("volume_m3"))
  , caption = "Ground Truth Piles: summary statistics for form measurements<br>ponderosa pine training site"
)

Table 2.1: Ground Truth Piles: summary statistics for form measurements
ponderosa pine training site

# piles	Metric	Mean	Std Dev	q 10%	Median	q 90%	Range
121	Height m	2.2	0.8	1.7	2.0	2.3	1.5—6.4
	Diameter m (image)	3.8	1.3	3.0	3.5	4.5	2.6—10.2
	Diameter m (field)	3.4	1.2	2.8	3.1	4.0	2.4—9.0
	Area m2 (image)	9.8	9.4	5.6	7.1	11.9	3.9—59.3
	Area m2 (field)	10.5	10.2	6.2	7.6	12.3	4.7—63.1

let’s check the field-collected and image-annotated measurements of diameter which will serve as a good sanity check for our image-annotation process (assuming diameter was accurately measured in the field…might be a perilous assumption)

slash_piles_polys %>% 
  dplyr::mutate(diff_diameter_m = image_gt_diameter_m - field_diameter_m) %>% 
  ggplot2::ggplot(mapping = ggplot2::aes(x = image_gt_diameter_m, y = field_diameter_m)) +
  ggplot2::geom_abline(lwd = 1.5) +
  ggplot2::geom_point(ggplot2::aes(color = diff_diameter_m)) +
  ggplot2::geom_smooth(method = "lm", se=F, color = "tomato", linetype = "dashed") +
  ggplot2::scale_color_viridis_c(option = "mako", direction = -1, alpha = 0.8) +
  ggplot2::scale_x_continuous(limits = c(0, max( max(slash_piles_polys$field_diameter_m,na.rm=T), max(slash_piles_polys$image_gt_diameter_m,na.rm=T) ) )) +
  ggplot2::scale_y_continuous(limits = c(0, max( max(slash_piles_polys$field_diameter_m,na.rm=T), max(slash_piles_polys$image_gt_diameter_m,na.rm=T) ) )) +
  ggplot2::labs(
    x = "image-annotated diameter (m)", y = "field-collected diameter (m)"
    , color = "image-field\ndiameter diff."
    , subtitle = "diameter (m) comparison"
  ) +
  ggplot2::theme_light()

the plot makes these values look very similar with the image-annotated diameter generally larger than the field-collected value. let’s check these using lm()

lm_temp <- lm(field_diameter_m ~ image_gt_diameter_m, data = slash_piles_polys)
summary(lm_temp)

## 
## Call:
## lm(formula = field_diameter_m ~ image_gt_diameter_m, data = slash_piles_polys)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.18985 -0.16525  0.01416  0.16807  1.76883 
## 
## Coefficients:
##                     Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          0.13522    0.09891   1.367    0.174    
## image_gt_diameter_m  0.86403    0.02436  35.471   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3593 on 119 degrees of freedom
##   (66 observations deleted due to missingness)
## Multiple R-squared:  0.9136, Adjusted R-squared:  0.9129 
## F-statistic:  1258 on 1 and 119 DF,  p-value: < 2.2e-16

Our slope of 0.86 is close to 1 and, along with our high R-squared value of 91%, indicate our image- and field-measured diameters are well-calibrated

let’s check the field-collected and image-annotated measurements of volume and area. for both volume measurements, a paraboloid geometry is assumed for calculation with the image-annotated volume relying on the field-collected heights

p1_temp <- slash_piles_polys %>% 
  ggplot2::ggplot(mapping = ggplot2::aes(x = image_gt_area_m2, y =field_gt_area_m2)) +
  ggplot2::geom_abline(lwd = 1.5) +
  ggplot2::geom_point(ggplot2::aes(color = height_m)) +
  ggplot2::geom_smooth(method = "lm", se=F, color = "tomato", linetype = "dashed") +
  ggplot2::scale_color_viridis_c(option = "mako", direction = -1, alpha = 0.8) +
  ggplot2::scale_x_continuous(limits = c(0, max( max(slash_piles_polys$field_gt_area_m2,na.rm=T), max(slash_piles_polys$image_gt_area_m2,na.rm=T) ) )) +
  ggplot2::scale_y_continuous(limits = c(0, max( max(slash_piles_polys$field_gt_area_m2,na.rm=T), max(slash_piles_polys$image_gt_area_m2,na.rm=T) ) )) +
  ggplot2::labs(
    x = "image-annotated area (m2)", y = "field-collected area (m2)"
    , color = "height (m)"
    , subtitle = "area (m2) comparison"
  ) +
  ggplot2::theme_light()
p2_temp <-
  slash_piles_polys %>% 
  ggplot2::ggplot(mapping = ggplot2::aes(x = image_gt_volume_m3, y =field_gt_volume_m3)) +
  ggplot2::geom_abline(lwd = 1.5) +
  ggplot2::geom_point(ggplot2::aes(color = height_m)) +
  ggplot2::geom_smooth(method = "lm", se=F, color = "tomato", linetype = "dashed") +
  ggplot2::scale_color_viridis_c(option = "mako", direction = -1, alpha = 0.8) +
  ggplot2::scale_x_continuous(limits = c(0, max( max(slash_piles_polys$field_gt_volume_m3,na.rm=T), max(slash_piles_polys$image_gt_volume_m3,na.rm=T) ) )) +
  ggplot2::scale_y_continuous(limits = c(0, max( max(slash_piles_polys$field_gt_volume_m3,na.rm=T), max(slash_piles_polys$image_gt_volume_m3,na.rm=T) ) )) +
  ggplot2::labs(
    x = "image-annotated volume (m3)", y = "field-collected volume (m3)"
    , color = "height (m)"
    , subtitle = "volume (m3) comparison"
  ) +
  ggplot2::theme_light()
patchwork::wrap_plots(list(p1_temp,p2_temp), guides = "collect") &
  ggplot2::theme(legend.position = "bottom")

even assuming a perfectly circular base for the area of the field-collected data (i.e. based on measured diameter), our image-annotated values are in-line with the field-collected data as we saw with the diameter comparison

quick summary of these measurements

slash_piles_polys %>% 
  sf::st_drop_geometry() %>% 
  dplyr::select(height_m, tidyselect::ends_with("area_m2"), tidyselect::ends_with("volume_m3")) %>% 
  summary()

##     height_m     image_gt_area_m2 field_gt_area_m2 image_gt_volume_m3
##  Min.   :1.524   Min.   : 3.805   Min.   : 4.670   Min.   :  3.279   
##  1st Qu.:1.829   1st Qu.: 6.200   1st Qu.: 6.585   1st Qu.:  5.963   
##  Median :1.981   Median : 7.107   Median : 7.591   Median :  7.088   
##  Mean   :2.179   Mean   :10.808   Mean   :10.486   Mean   : 13.831   
##  3rd Qu.:2.134   3rd Qu.: 8.597   3rd Qu.: 8.829   3rd Qu.:  8.428   
##  Max.   :6.401   Max.   :60.998   Max.   :63.069   Max.   :172.950   
##  NA's   :66                       NA's   :66       NA's   :66        
##  field_gt_volume_m3
##  Min.   :  4.270   
##  1st Qu.:  6.615   
##  Median :  7.527   
##  Mean   : 14.990   
##  3rd Qu.:  8.746   
##  Max.   :183.080   
##  NA's   :66

2.2 RGB orthomosaic

Orthomosaic tif files from the UAS flight imagery that were created in Agisoft Metashape are loaded and stitched together via terra::mosaic.

  # read list of orthos
  ortho_list_temp <- list.files(
    "f:\\PFDP_Data\\p4pro_images\\P4Pro_06_17_2021_half_half_optimal\\3_dsm_ortho\\2_mosaic"
    , pattern = "*\\.(tif|tiff)$", full.names = T)[] %>% 
    purrr::map(function(x){terra::rast(x)})
  
  ortho_list_temp[[1]] %>% terra::res()
  #   terra::aggregate(20) %>%
  #   terra::plotRGB(r = 1, g = 2, b = 3, stretch = "hist", colNA = "transparent")
  
  ####### ensure the resolution of the rasters matches 
    # terra::res(ortho_list_temp[[1]])
    
    ## function
    change_res_fn <- function(r, my_res=1, m = "bilinear"){
      r2 <- r
      terra::res(r2) <- my_res
      r2 <- terra::resample(r, r2, method = m)
      return(r2)
    }
    ## apply the function
    ortho_list_temp <- 1:length(ortho_list_temp) %>% 
      purrr::map(function(x){change_res_fn(ortho_list_temp[[x]], my_res=0.10)})
    
    # terra::res(ortho_list_temp[[1]])
    
    # ortho_list_temp[[1]] %>%
    #   terra::aggregate(2) %>%
    #   terra::plotRGB(r = 1, g = 2, b = 3, stretch = "hist", colNA = "transparent")

  ######## mosaic the raster list 
    ortho_rast <- terra::mosaic(
      terra::sprc(ortho_list_temp)
      , fun = "min" # min only thing that works
    ) 
    
    names(ortho_rast) <- c("red","green","blue","alpha")
    
  # ortho_rast %>%
  #   terra::aggregate(4) %>%
  #   terra::plotRGB(r = 1, g = 2, b = 3, stretch = "lin", colNA = "transparent")

make a function to plot the RGB imagery as a background for ggplot2 plots

######################################################################################
# function to plot ortho + stand
######################################################################################
ortho_plt_fn = function(my_ortho_rast = ortho_rast, stand = las_ctg_dta %>% sf::st_union() %>% sf::st_as_sf(), buffer = 20){
# convert to stars
  ortho_st <- my_ortho_rast %>%  
    terra::subset(subset = c(1,2,3)) %>%
    terra::crop(
      stand %>% sf::st_buffer(buffer) %>% terra::vect()
    ) %>% 
    # terra::aggregate(fact = 2, fun = "mean", na.rm = T) %>% 
    stars::st_as_stars()
  
  # convert to rgb
  ortho_rgb <- stars::st_rgb(
    ortho_st[,,,1:3]
    , dimension = 3
    , use_alpha = FALSE
    # , stretch = "histogram"
    , probs = c(0.005, 0.995)
    , stretch = "percent"
  )
  # ggplot
  plt_rgb <- ggplot2::ggplot() +
    stars::geom_stars(data = ortho_rgb[]) +
    ggplot2::scale_fill_identity(na.value = "transparent") + # !!! don't take this out or RGB plot will kill your computer
    ggplot2::scale_x_continuous(expand = c(0, 0)) +
    ggplot2::scale_y_continuous(expand = c(0, 0)) +
    ggplot2::labs(
      x = ""
      , y = ""
    ) +
    ggplot2::theme_void()
  
  # return(plt_rgb)
  # combine all plot elements
  plt_combine = plt_rgb +
    # geom_sf(
    #   data = stand
    #   , alpha = 0
    #   , lwd = 1.5
    #   , color = "gray22"
    # ) +
    ggplot2::theme(
      legend.position = "top" # c(0.5,1)
      , legend.direction = "horizontal"
      , legend.margin = ggplot2::margin(0,0,0,0)
      , legend.text = ggplot2::element_text(size = 8)
      , legend.title = ggplot2::element_text(size = 8)
      , legend.key = ggplot2::element_rect(fill = "white")
      # , plot.title = ggtext::element_markdown(size = 10, hjust = 0.5)
      , plot.title = ggplot2::element_text(size = 8, hjust = 0.5, face = "bold")
      , plot.subtitle = ggplot2::element_text(size = 6, hjust = 0.5, face = "italic")
    )
  return(plt_combine)
}

plot an example slash pile RGB image

stand_temp <- slash_piles_polys %>%
    dplyr::filter(tolower(comment)=="mechanical pile") %>% 
    dplyr::arrange(desc(field_diameter_m)) %>% 
    dplyr::slice(1) %>% 
    sf::st_point_on_surface() %>% 
    sf::st_buffer(10, endCapStyle = "SQUARE") %>% 
    sf::st_transform(terra::crs(ortho_rast))
# check it with the ortho
ortho_plt_fn(stand = stand_temp)

ggsave("../data/pile_rgb.jpeg", height = 5, width = 5)

2.2.1 Example ratio-based index

While hyperspectral image data enables more detailed analysis by capturing a broader spectral range than RGB imagery, we can still perform robust analysis using spectral data in the visible range

let’s define a general function for a ratio based (e.g. vegetation) index

spectral_index_fn <- function(rast, layer1, layer2) {
  bk <- rast[[layer1]]
  bi <- rast[[layer2]]
  vi <- (bk - bi) / (bk + bi)
  return(vi)
}

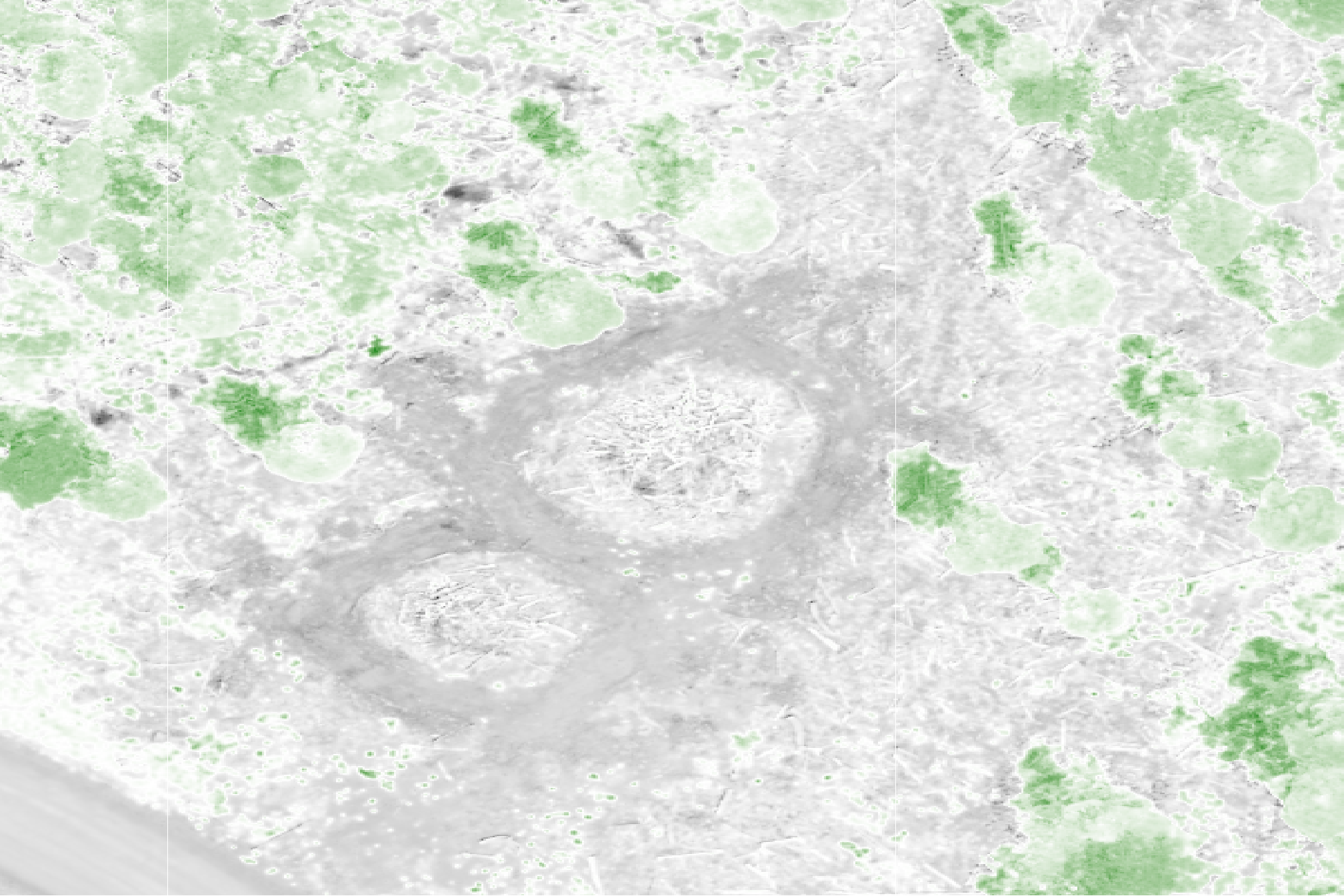
The Green-Red Vegetation Index (GRVI) uses the reflectance of green and red bands to assess vegetation health and identify ground cover types. The formula is GRVI = (green - red) / (green + red). Higher GRVI values indicate healthy vegetation, while negative values suggest soils, and values near zero may indicate water or snow.

grvi_rast <- spectral_index_fn(rast = ortho_rast, layer1 = 2, layer2 = 1)
names(grvi_rast) <- c("grvi")
terra::plot(grvi_rast, col = harrypotter::hp(n=100, option = "Slytherin"))

let’s check the GRVI for a ground truth pile

# check it with the ortho
grvi_rast %>% 
  terra::crop(stand_temp %>% sf::st_buffer(20)) %>% 
  terra::as.data.frame(xy=T) %>% 
  dplyr::rename(f=3) %>% 
  ggplot2::ggplot() +
  ggplot2::geom_tile(ggplot2::aes(x=x,y=y,fill = f), color = NA) +
  scale_fill_gradient2(low = "black", high = "forestgreen") +
  scale_x_continuous(expand = c(0, 0)) +
  scale_y_continuous(expand = c(0, 0)) +
  ggplot2::theme_void() +
  theme(
      legend.position = "none" # c(0.5,1)
      , legend.direction = "horizontal"
      , legend.margin = margin(0,0,0,0)
      , legend.text = element_text(size = 8)
      , legend.title = element_text(size = 8)
      , legend.key = element_rect(fill = "white")
      # , plot.title = ggtext::element_markdown(size = 10, hjust = 0.5)
      , plot.title = element_text(size = 10, hjust = 0.5, face = "bold")
      , plot.subtitle = element_text(size = 8, hjust = 0.5, face = "italic")
    )

ggsave("../data/pile_grvi.jpeg", height = 5, width = 5)

2.3 Study area imagery

let’s look at the RGB imagery and pile locations

# get the base plot
plt_rgb_ortho <- ortho_plt_fn(
  stand = 
    slash_piles_points %>% 
    sf::st_bbox() %>% 
    sf::st_as_sfc() %>% 
    sf::st_buffer(50) %>% 
    sf::st_transform(terra::crs(ortho_rast))
)
# add pile locations
plt_rgb_ortho +
  ggplot2::geom_sf(
    data = slash_piles_points %>% sf::st_transform(terra::crs(ortho_rast))
    , ggplot2::aes() # size = diameter
    , shape = 1
    , color = "firebrick"
  ) +
  ggplot2::theme(legend.position = "none")

notice these are point measurements of plot locations and the points are not precisely in the center of the pile. notice also there are piles in the imagery that were not measured (e.g. upper-left corner)

we created image-annotated pile polygons using the RBG and field-collected pile location data to compare against our predicted slash pile segments using an intersection over union (IoU) approach

let’s make a panel of plots for each pile

p_fn_temp <- function(
    rn
    , df = slash_piles_polys %>% dplyr::filter(!is.na(comment))
    , crs = terra::crs(ortho_rast)
) {
  # scale the buffer based on the largest
  d <- df %>%
    dplyr::arrange(tolower(comment), desc(field_diameter_m)) %>% 
    dplyr::slice(rn) %>% 
    sf::st_transform(crs)
  # plt
  ortho_plt_fn(stand=d) + 
    ggplot2::geom_sf(data = d, fill = NA, color = "firebrick") +
    ggplot2::labs(
      subtitle = paste0(
        tolower(d$comment)
        , "\ndiam. = "
        , scales::comma(d$field_diameter_m, accuracy = 0.1)
        # , ", ht. = "
        # , scales::comma(d$height, accuracy = 0.1)
      )
    )
}
# add pile locations
plt_list_rgb <- 1:nrow(slash_piles_polys %>% dplyr::filter(!is.na(comment))) %>% 
  purrr::map(p_fn_temp)

plot tiles

patchwork::wrap_plots(
  sample(
    plt_list_rgb, size = as.integer(nrow(slash_piles_points)/3))
  , ncol = 5
)

ggsave("../data/pile_tiles_rgb.jpeg", height = 10.5, width = 8)

a challenge in using the spectral data to identify slash piles will be to develop a spectral-based method that can account for the different lighting conditions in the imagery (e.g. piles in shadows or under tree crowns). this different lighting may have also influenced the point cloud generation

2.4 Point Cloud Data

Let’s check out the point cloud data we got using UAS-SfM methods

# directory with the downloaded .las|.laz files
f_temp <- 
  "f:\\PFDP_Data\\p4pro_images\\P4Pro_06_17_2021_half_half_optimal\\2_densification\\point_cloud"
  # system.file(package = "lidR", "extdata", "Megaplot.laz")
# is there data?
list.files(f_temp, pattern = ".*\\.(laz|las)$") %>% length()

## [1] 1

# what files are in here?
list.files(f_temp, pattern = ".*\\.(laz|las)$")[1]

## [1] "P4Pro_06_17_2021_half_half_optimal_group1_densified_point_cloud.las"

what information does lidR read from the catalog?

las_ctg <- lidR::readLAScatalog(f_temp)
# set the processing options
lidR::opt_progress(las_ctg) <- F
lidR::opt_filter(las_ctg) <- "-drop_duplicates"
lidR::opt_select(las_ctg) <- "xyziRGB"
# huh?
las_ctg

## class       : LAScatalog (v1.2 format 3)
## extent      : 499264.2, 499958.8, 4317541, 4318147 (xmin, xmax, ymin, ymax)
## coord. ref. : WGS 84 / UTM zone 13N 
## area        : 420912.1 m²
## points      : 158.01 million points
## type        : terrestrial
## density     : 375.4 points/m²
## num. files  : 1

that’s a lot of points…can an ordinary laptop handle it? we’ll find out.

We’ll plot our point cloud data tiles real quick to orient ourselves

las_ctg %>% 
  purrr::pluck("data") %>% 
  mapview::mapview(popup = F, layer.name = "point cloud tile")

2.5 Check out one pile

las_temp <- lidR::clip_roi(
  las_ctg
  # biggest mechanical
  , slash_piles_polys %>%
    dplyr::filter(tolower(comment)=="mechanical pile") %>% 
    dplyr::arrange(desc(field_diameter_m)) %>% 
    dplyr::slice(1) %>% 
    sf::st_point_on_surface() %>% 
    sf::st_buffer(10, endCapStyle = "SQUARE") %>% 
    sf::st_transform(lidR::st_crs(las_ctg))
)

what did we get?

las_temp@data %>% dplyr::glimpse()

## Rows: 181,073
## Columns: 7
## $ X         <dbl> 499807.3, 499807.3, 499807.3, 499807.3, 499807.3, 499807.3, …
## $ Y         <dbl> 4317993, 4317992, 4317983, 4317983, 4317993, 4317989, 431799…
## $ Z         <dbl> 2711.213, 2711.567, 2713.496, 2713.221, 2711.405, 2712.323, …
## $ Intensity <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ R         <int> 40448, 33024, 37632, 40192, 17152, 42496, 41472, 39168, 5068…
## $ G         <int> 37632, 31232, 35584, 36864, 16384, 38912, 37632, 37376, 5273…
## $ B         <int> 33280, 26112, 29184, 31744, 10752, 34304, 32256, 33792, 5145…

plot a sample

las_temp %>% 
  lidR::plot(
    color = "Z", bg = "white", legend = F
   , pal = harrypotter::hp(n=50, house = "gryffindor")
  )

make a gif

library(magick)
if(!file.exists(file.path("../data/", "pile_z.gif"))){
  rgl::close3d()
  lidR::plot(
    las_temp, color = "Z", bg = "white", legend = F
   , pal = harrypotter::hp(n=50, house = "gryffindor")
  )
  rgl::movie3d( rgl::spin3d(), duration = 10, fps = 10 , movie = "pile_z", dir = "../data/")
  rgl::close3d()
}

library(magick)
if(!file.exists(file.path("../data/", "pile_rgb.gif"))){
  rgl::close3d()
  lidR::plot(
    las_temp, color = "RGB", bg = "white", legend = F
  )
  rgl::movie3d( rgl::spin3d(), duration = 10, fps = 10 , movie = "pile_rgb", dir = "../data/")
  rgl::close3d()
}